ეს პროდუქტი წარმატებით დაემატა კალათას!
პრიზმის ოპტიკა
| მოდელი | ტიპი | განზომილება | საფარი | ეფექტური დიაფრაგმა | ერთეულის ფასი | ||
|---|---|---|---|---|---|---|---|
| მეტი+ნაკლები- | CH9038A00001 | მტრედის პრიზმები | A21.1 მმ*B5 მმ*H5 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9038A00002 | მტრედის პრიზმები | A42.3 მმ*B10 მმ*H10 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9038A00003 | მტრედის პრიზმები | A63.4 მმ*B15 მმ*H15 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
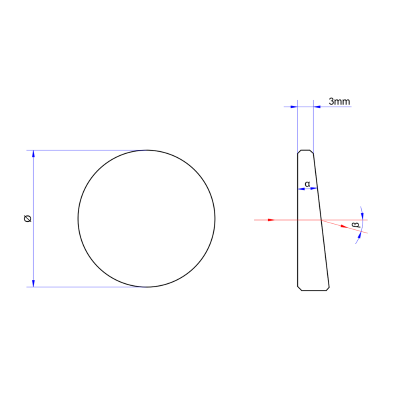
| მეტი+ნაკლები- | CH9041A00001 | სოლისებრი პრიზმები | α=2°4'*Φ25.4 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9041A00002 | სოლისებრი პრიზმები | α=4°7'*Φ25.4 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9041A00003 | სოლისებრი პრიზმები | α=8°14'*Φ25.4 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9041A00004 | სოლისებრი პრიზმები | α=1°57'*Φ25.4 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9041A00005 | სოლისებრი პრიზმები | α=3°53'*Φ25.4 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9041A00006 | სოლისებრი პრიზმები | α=7°41'*Φ25.4 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9039A00001 | Amici-ის სახურავის პრიზმები | A15 მმ*B15 მმ*H12 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9039A00002 | Amici-ის სახურავის პრიზმები | A23 მმ*B23 მმ*H18 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9039A00003 | Amici-ის სახურავის პრიზმები | A31.5 მმ B31.5 მმ * H23 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9037A00001 | მართკუთხა პრიზმები | 5 მმ (ა=ბ=გ) | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9037A00002 | მართკუთხა პრიზმები | 10 მმ (ა=ბ=გ) | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9037A00003 | მართკუთხა პრიზმები | 12.7 მმ (ა=ბ=გ) | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9037A00004 | მართკუთხა პრიზმები | 15 მმ (ა=ბ=გ) | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9037A00005 | მართკუთხა პრიზმები | 20 მმ (ა=ბ=გ) | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9037A00006 | მართკუთხა პრიზმები | 25.4 მმ (ა=ბ=გ) | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9036A00001 | კუთხის კუბის რეტროარეკლის პრიზმა | Φ15 მმ*H11.3 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9036A00002 | კუთხის კუბის რეტროარეკლის პრიზმა | Φ25.4 მმ*H19 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9036A00003 | კუთხის კუბის რეტროარეკლის პრიზმა | Φ38 მმ*H28.5 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9036A00004 | კუთხის კუბის რეტროარეკლის პრიზმა | Φ50.8 მმ*H37.5 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
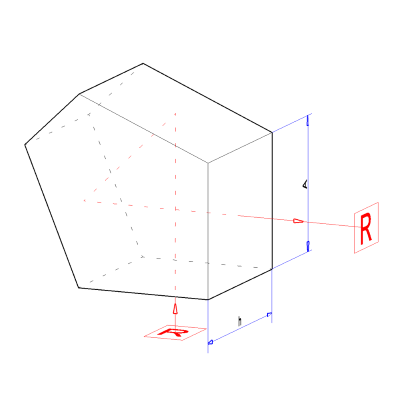
| მეტი+ნაკლები- | CH9035A00001 | პენტა პრიზმები | 2.5 მმ*2.5 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9035A00002 | პენტა პრიზმები | 7 მმ*6 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9035A00003 | პენტა პრიზმები | 10 მმ*10 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9035A00004 | პენტა პრიზმები | 15 მმ*15 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
| მეტი+ნაკლები- | CH9035A00005 | პენტა პრიზმები | 20 მმ*20 მმ | დაუფარავი | >80% | ციტატის მოთხოვნა | |
პრიზმები გამჭვირვალე ოპტიკური ელემენტებია ბრტყელი, გაპრიალებული ზედაპირით, რომლებსაც შეუძლიათ სინათლის გავლისას მისი მანიპულირება. ისინი ხშირად დამზადებულია შუშის ან სხვა გამჭვირვალე მასალისგან, განსხვავებული გარდატეხის ინდექსით.
პრიზმები ფართოდ გამოიყენება სხვადასხვა ოპტიკურ სისტემებსა და მოწყობილობებში სინათლის სამართავად და მანიპულირებისთვის, მათ შორის კამერებში, ბინოკლებში, მიკროსკოპებში, ტელესკოპებში, სპექტროსკოპებში და სხვა. ისინი გადამწყვეტ როლს ასრულებენ სინათლის მიმართულების, დისპერსიისა და პოლარიზაციის შეცვლაში, რაც მათ ოპტიკურ ინჟინერიასა და სამეცნიერო კვლევებში ღირებულ კომპონენტებად აქცევს.
აქ მოცემულია პრიზმების რამდენიმე გავრცელებული ტიპი და მათი გამოყენება:
მართკუთხა პრიზმაამ პრიზმას ორი პერპენდიკულარული ზედაპირი აქვს და ხშირად გამოიყენება სინათლის 90 გრადუსით გადახრისთვის. ისინი ფართოდ გამოიყენება გეოდეზიურ მოწყობილობებსა და პერისკოპებში.
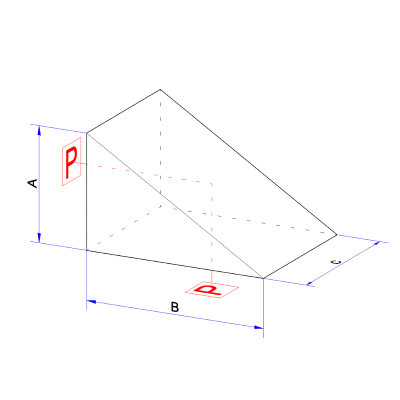
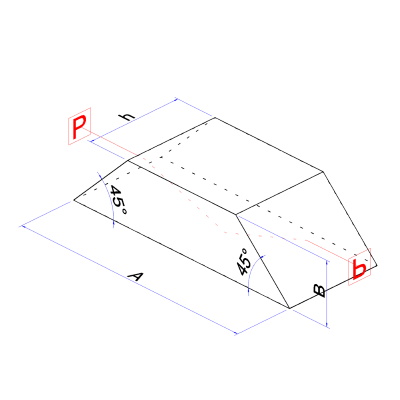
პოროს პრიზმაბინოკლებში გამოყენებული პოროს პრიზმები ხელს უწყობს კომპაქტური და დაკეცილი ოპტიკური ბილიკის შექმნას, რაც კომპაქტურ კორპუსში უფრო გაფართოებული ოპტიკური ბილიკის შექმნის საშუალებას იძლევა.
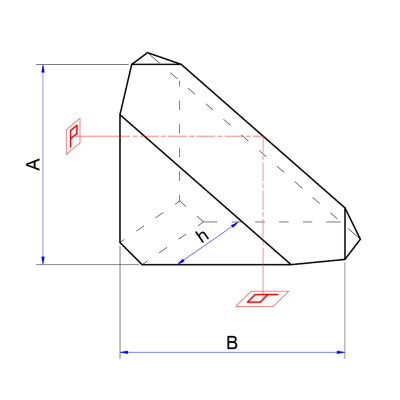
მტრედის პრიზმამტრედისებრ პრიზმებს უჩვეულო ფორმა აქვთ, რაც მათ საშუალებას აძლევს, გამოსახულება 180 გრადუსით შეცვალონ ან გადაატრიალონ. ისინი სხვადასხვა ოპტიკურ ინსტრუმენტებსა და ლაზერულ აპლიკაციებში გამოიყენება.
დისპერსიული პრიზმებიეს პრიზმები შექმნილია სინათლის შემადგენელ ფერებად დაყოფისთვის მათი ტალღის სიგრძის მიხედვით. ისინი სპექტროსკოპიისა და ფერებთან დაკავშირებული სხვა აპლიკაციების ფუნდამენტური კომპონენტებია.
ამიჩი პრიზმაამ ტიპის პრიზმა ხშირად გვხვდება სადემონსტრაციო ტელესკოპებსა და ტელესკოპებში, რადგან ის ასწორებს გამოსახულების ორიენტაციას, რაც უზრუნველყოფს ვერტიკალურ და სწორად ორიენტირებულ გამოსახულებას.
სახურავის პრიზმასახურავის პრიზმები ბინოკლებში გამოიყენება თხელი და სწორხაზოვანი დიზაინის შესაქმნელად. ისინი უფრო კომპაქტური ფორმის ფაქტორის საშუალებას იძლევა.
პრიზმები მრავალმხრივი ოპტიკური ელემენტებია, რომლებიც საუკუნეების განმავლობაში გამოიყენება და სინათლის ზუსტი კონტროლის უნარი მათ ფასდაუდებელს ხდის ოპტიკური სისტემების ფართო სპექტრსა და სამეცნიერო ექსპერიმენტებში.პრიზმის ოპტიკაგულისხმობს მათი თვისებების, სინათლის სხვადასხვა ტალღის სიგრძეებთან ქცევის გაგებას და მათ ინტეგრაციას სხვადასხვა ოპტიკურ დიზაინში კონკრეტული მიზნების მისაღწევად.
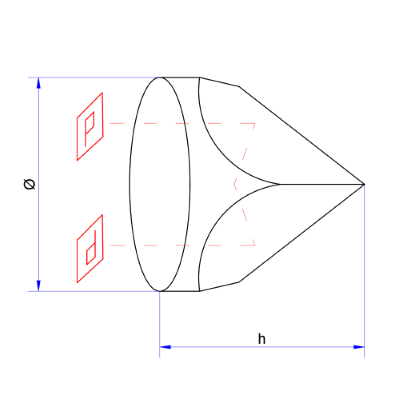 კუთხის კუბის რეტროარეკლის პრიზმა
კუთხის კუბის რეტროარეკლის პრიზმა
-

სკაიპი
-

WhatsApp
-

ზედა
- English
- French
- German
- Portuguese
- Spanish
- Russian
- Japanese
- Korean
- Arabic
- Irish
- Greek
- Turkish
- Italian
- Danish
- Romanian
- Indonesian
- Czech
- Afrikaans
- Swedish
- Polish
- Basque
- Catalan
- Esperanto
- Hindi
- Lao
- Albanian
- Amharic
- Armenian
- Azerbaijani
- Belarusian
- Bengali
- Bosnian
- Bulgarian
- Cebuano
- Chichewa
- Corsican
- Croatian
- Dutch
- Estonian
- Filipino
- Finnish
- Frisian
- Galician
- Georgian
- Gujarati
- Haitian
- Hausa
- Hawaiian
- Hebrew
- Hmong
- Hungarian
- Icelandic
- Igbo
- Javanese
- Kannada
- Kazakh
- Khmer
- Kurdish
- Kyrgyz
- Latin
- Latvian
- Lithuanian
- Luxembou..
- Macedonian
- Malagasy
- Malay
- Malayalam
- Maltese
- Maori
- Marathi
- Mongolian
- Burmese
- Nepali
- Norwegian
- Pashto
- Persian
- Punjabi
- Serbian
- Sesotho
- Sinhala
- Slovak
- Slovenian
- Somali
- Samoan
- Scots Gaelic
- Shona
- Sindhi
- Sundanese
- Swahili
- Tajik
- Tamil
- Telugu
- Thai
- Ukrainian
- Urdu
- Uzbek
- Vietnamese
- Welsh
- Xhosa
- Yiddish
- Yoruba
- Zulu
- Kinyarwanda
- Tatar
- Oriya
- Turkmen
- Uyghur



 პროდუქტები
პროდუქტები